You are here:

Fixed and random effects models for panel data in Stata

Presenter(s): Kevin Ralston


decorative image to accompany text

This resource introduces examples of fixed and random effects models using the software Stata. Random and fixed effect models are also known as panel data models because they take account of the multiple measurement points of individuals measured in panel data. These models are introduced and compared to a standard regression model, regression where clustering is accounted for and also the Mundlak model and Allison’s (2009) Hybrid model, which combine both fixed and random effects. 

Fixed and random effect models

The fixed effect model ‘treats unobserved differences between individuals as a set of fixed parameters that can either be directly estimated or partialed out of estimating equations’ (Allison 2009, p. 2).



   Download transcript    |   Download slides [ Views ]

The fixed effect controls for all stable unobserved variables. This includes variables that have not, or cannot, be measured. This is because each individual becomes their own control. Because of this all within individual variation is accounted for in the fixed effect. All time invariant differences between individuals are contained in the fixed effect and time varying differences can be estimated in the model. There is a major drawback with the fixed effect approach, however. That is, because all time invariant differences between individuals are incorporated in the fixed effect we cannot estimate time invariant parameters within a fixed effect framework.

Fixed effect model:


Fixed effect model (downlaos PowerPoint slide for accessibiliy):

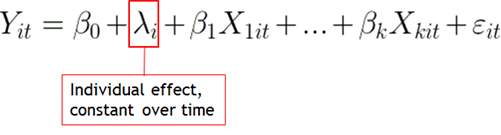
> Download this model in an accessible PowerPoint slide.

Allison (2009) argues that what distinguishes the random effects approach from the fixed effects approach is defined by the structure of the association between observed and unobserved variables. In the random effects framework there are two components to the error distribution (this is why historically in some of the literature it is known as an error components model). This leads to a requirement to assume that unobserved variables are uncorrelated with the observed variables. This assumption means that unobserved characteristics must be uncorrelated with the variables that are observed in the model (correlation between the observed and unobserved variables may lead to bias the random effects estimates).

Random effect model:


random effect model (downlaos PowerPoint slide for accessibiliy):

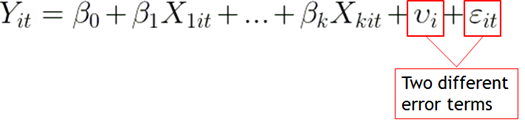
> Download this model in an accessible PowerPoint slide.


Comparing the fixed effect and random effect model


   Download transcript    |   Download slides [ Views ]

It is common practice to compare fixed and random effects models using a Hausman test. Rabe-Hesketh and Skrondal (2008) provide a technical explanation of the Hausman test. Allison (2009) provides a pithy definition of the Hausman test, explaining that Hausman tests the hypothesis that the FE coefficients are identical to the RE. If they are identical, then ordinarily we would prefer the random effects model because it also provides correct standard errors. If they are not, then we may prefer the fixed effects model because, theoretically, the coefficients are considered to be unbiased (i.e. consistent).

In summary, the fixed effect model summarises patterns of change within individuals. The unbiased estimates mean that this model is sometimes described as consistent. The random effects panel model is using (or borrowing) some information from the fixed effects panel model, at the same time as borrowing some information from the between effects model. This approach may sometimes be referred to as efficient because it does not discard as much information as the fixed effect model. The orthodox position is that it is likely that a correlation between unobserved and observed variables in the random effects approach will bias estimates, although recent work questions this position (e.g. Bell 2015). 



   Download transcript    |   [ Views ]

> Download the .do file exercise.


Choosing a fixed or random effect model

There is substantial debate within the methodological literature over the optimal application of fixed or random effects. There is a growing body of work demonstrating the possibility of estimating consistent fixed effect style estimates within a random effects framework. For example, Mundlak (1978) showed that the inclusion of cluster means for all within individual covariates can enable consistent estimation of within effects in a random effects framework. 

Allison (2009) put forward a ‘hybrid model’ similar to that suggested by Mundlak (1978) using a group mean centring approach. Bell et al. (2019) similarly suggest an approach where is divided into two parts, each with a separate effect. One part represents the average within effect of X it the second part represents the average between effect of X it. An additional parameter represents the effect of time-invariant variables, a between effect. 

In undertaking analysis researchers should proceed by thinking about their research question and the scope and limitations of the available data. Where possible, the choice between the fixed effects panel model and the random effects panel model should be informed by your theoretical understanding of the social process that is being analysed. Researchers are advised to estimate a series of theoretically plausible statistical models and carefully compare their results. It is also sensible to consider extensions to the random effects model such as the Mundlak approach or the hybrid model. A clear statement should be made justifying the choice of model and the results should be made available within the auxiliary information on the data analytical process, for example in an appendix posted in a repository.

> Download extended examples (a PDF document).

 

___

References

Allison, P.D. (2009) Fixed Effects Regression Models. vol. 160. SAGE publications

Bell, A., & Jones, K. (2015). Explaining fixed effects: Random effects modeling of time-series cross-sectional and panel data. Political Science Research and Methods, 3(1), 133-153.

Bell, A., Fairbrother, M., and Jones, K. (2019) ‘Fixed and Random Effects Models: Making an Informed Choice’. Quality & Quantity 53 (2), 1051–1074

Gayle, V. and Lambert, P. (2018) What Is Quantitative Longitudinal Data Analysis? Bloomsbury Publishing

Mundlak, Y. (1978) ‘On the Pooling of Time Series and Cross Section Data’. Econometrica: Journal of the Econometric Society 69–85

Rabe-Hesketh, S. and Skrondal, A. (2008) Multilevel and Longitudinal Modeling Using Stata. STATA press




Supporting materials

About the author

Dr. Kevin Ralston is a Lecturer in Sociology and Quantitative Methods and Director of the Edinburgh Q-Step Centre. He has published widely, using quantitative methods to study inequality. In addition to substantively focussed sociologically relevant research, Kevin has led in the production of pedagogical study into the learning-teaching of quantitative methods. 

Primary author profile page


⌃
BACK TO TOP